Longest Common Sequence: Algorithm & Applications

Understanding the Longest Common Subsequence Algorithm

The Longest Common Subsequence (LCS) refers to the longest sequence that appears in both given sequences in the same order, but not necessarily consecutively. For example, for sequences "ABCDEF" and "AEBDF", the LCS is "ABDF".

Defining Subsequence

A subsequence is a sequence derived from another sequence by deleting some (or no) elements without changing the order of the remaining elements. In LCS, the subsequence maintains the sequence’s original order.

Difference from Substring

A substring is contiguous, whereas a subsequence can have gaps. This makes LCS more flexible, allowing it to uncover relationships not visible through contiguous patterns.

Examples of LCS

• Sequences: "AGGTAB" and "GXTXAYB"
• LCS: "GTAB"
  Despite non-consecutive characters, the order is maintained.

Importance in Sequence Alignment

Role in Bioinformatics

LCS is crucial in comparing DNA, RNA, or protein sequences. It helps infer evolutionary relationships, understand functional similarities, and predict the effects of genetic mutations.

Applications in Text Editing

In text editing and processing, LCS identifies differences and similarities between documents, making it useful in version control systems and collaborative work.

Enhancing Data Processing

LCS aids tasks like data deduplication, ensuring storage efficiency by eliminating redundant information.

How the Longest Common Subsequence Algorithm Works

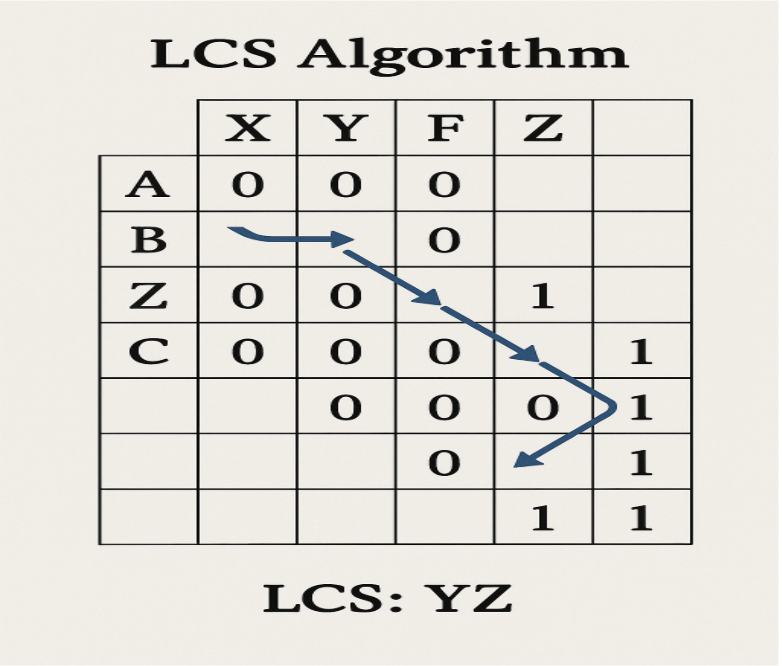
The LCS algorithm uses dynamic programming to efficiently find the longest common subsequence between two sequences.

Step 1: Create a Matrix

• Rows represent the first sequence, columns the second.
• Matrix size: (m+1) x (n+1) where m and n are sequence lengths.

Importance of Matrix Representation

Each cell represents a subproblem, enabling incremental solution building and handling large datasets efficiently.

Initialization and Base Cases

• Fill the first row and column with zeros.
• Handles cases where one sequence is empty, providing a foundation for dynamic programming.

Step 2: Fill the Matrix

For each cell:

• If characters match: cell value = diagonal cell + 1
• If characters don’t match: cell value = max(top cell, left cell)

Character Comparison Logic

• Diagonal values extend the subsequence when characters match.
• Maximum of top/left preserves the longest subsequence found so far.

Step 3: Trace Back to Find the LCS

• Start from the bottom-right cell.
• If characters match → move diagonally up-left, adding to LCS.
• If not → move in the direction of the larger adjacent value.

Tracing Back: A Reverse Journey

Retracing the matrix reconstructs the longest subsequence, confirming correctness.

Building the LCS

Matched characters are accumulated step-by-step, forming the final LCS sequence.

Example of the LCS Algorithm

• Sequences: "ABCBDAB" and "BDCAB"
• Steps:
  1. Create and initialize an 8×6 matrix
  2. Fill the matrix comparing characters
  3. Trace back → LCS = "BCAB"

Applications of the Longest Common Subsequence

Bioinformatics

• Evolutionary Insights: Trace evolutionary paths and construct phylogenetic trees
• Functional Genomics: Identify conserved regions across species
• Genetic Mutation Analysis: Detect variations that may lead to disorders

Text Comparison

• Document Versioning: Track changes in software or collaborative writing
• Plagiarism Detection: Identify copied content
• Text Data Analysis: Detect recurring themes for content strategy

Data Compression

• Redundancy Reduction: Remove duplicate data for smaller file sizes
• Enhancing Storage Efficiency: Maximize storage by retaining only unique data
• Compression in Multimedia: Reduce sizes of audio, video, and image files while maintaining quality

Conclusion

The LCS algorithm is a cornerstone for sequence alignment and data comparison. By mastering it, you gain:

• Insight into bioinformatics, text editing, and data optimization
• A strong foundation in dynamic programming
• The ability to handle complex pattern recognition tasks efficiently

Embracing Algorithmic Efficiency

Dynamic programming ensures LCS handles large datasets optimally.

Broadening Application Horizons

From AI to cybersecurity, LCS identifies patterns and similarities, driving innovation.

Future Prospects

As technology evolves, LCS remains a robust, adaptable tool for analyzing and comparing sequences across diverse domains.