Mastering Longest Common Subsequence Algorithm

Understanding the Longest Common Subsequence Algorithm

The Longest Common Subsequence (LCS) algorithm is a fundamental concept in computer science that identifies the longest subsequence common to two sequences. It is widely used in bioinformatics, text comparison, and version control systems. This guide explores the LCS concept, algorithm, and its applications in real-world scenarios.

Definition and Basic Concepts

A subsequence is derived from another sequence by deleting some elements without changing the order of the remaining elements.

Example:
Sequence: ABCDEF
Possible subsequences: ABC, ACE, BDF, etc.

The key property is maintaining the relative order, which makes subsequences valuable for analyzing sequences for common patterns.

Example of Longest Common Subsequences

The LCS is the longest subsequence that two sequences share.

Example:

• Sequence 1: ABCDGH
• Sequence 2: AEDFHR
• LCS: ADH (Length = 3)

Note: LCS may not be unique; multiple subsequences of the same maximum length may exist.

Importance of LCS

Bioinformatics Applications

• Comparing DNA, RNA, and protein sequences.
• Inferring evolutionary relationships.
• Identifying functional regions in genetic material.

Text Processing and File Comparison

• Used in diff utilities to highlight differences between files.
• Facilitates document revision, code comparison, and content management.

Version Control Systems

• Tracks changes between file versions.
• Helps developers resolve conflicts and maintain a coherent project history.

String Matching Problems

• Useful in data analysis and pattern recognition.
• Enables efficient identification of common subsequences in large datasets.

How the Longest Common Subsequence Algorithm Works

Dynamic Programming Approach

Dynamic programming provides an efficient solution to LCS by storing results of subproblems to avoid redundant computations, unlike brute force solutions.

Step-by-Step Explanation

Step 1: Creating the 2D Table

• Set up a table with dimensions (m+1) x (n+1) where m and n are the lengths of the sequences.
• Each cell (i, j) stores the LCS length of sequences up to i-th and j-th indices.

Step 2: Initializing the Table

• Fill the first row and column with zeros.
• Handles edge cases where one sequence is empty.

Step 3: Filling the Table

• For each cell (i, j):
  • If characters match: cell(i,j) = 1 + cell(i-1,j-1)
  • Else: cell(i,j) = max(cell(i-1,j), cell(i,j-1))

Step 4: Traceback to Find LCS

• Start from the bottom-right cell (m, n) to reconstruct the LCS.
• If characters match, move diagonally up-left; otherwise, move towards the larger adjacent value.
• Collect matched characters along the path to form the final LCS.

Example of LCS Calculation

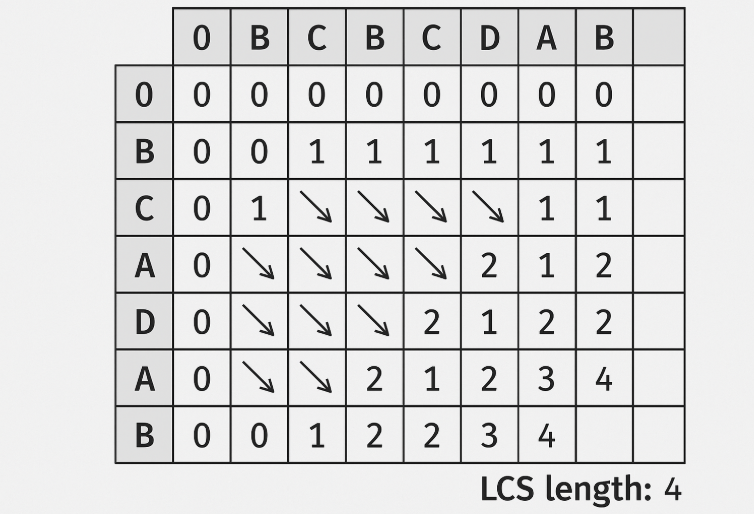
• Sequences: ABCBDAB and BDCAB
• Create 2D table: 8×6 (extra row/column for zeros)
• Fill table using matching rules.
• Traceback → LCS = BCAB

This demonstrates the efficiency of dynamic programming in computing LCS.

Applications of Longest Common Subsequence

Text Comparison Tools

• Highlights differences between document versions.
• Useful for proofreading, code review, and collaborative editing.

Bioinformatics Analysis

• Compares DNA, RNA, and protein sequences.
• Infers evolutionary pathways and identifies functional regions.

Data Versioning in Software Development

• Highlights code changes between versions.
• Facilitates collaboration and conflict resolution in development teams.

Enhancing Collaboration and Productivity

• Provides insights into sequence similarities.
• Streamlines workflows and decision-making in research and development.

Conclusion

The Longest Common Subsequence algorithm is a cornerstone for sequence comparison and data analysis. By using dynamic programming, it efficiently identifies common subsequences, enabling applications in:

• Bioinformatics
• Text processing
• Version control

Mastering LCS enhances your ability to analyze, compare, and manage data, making it an indispensable tool in computational tasks and modern technology.